INECUACIONES LINEALES.
Concepto.- Las inecuaciones son desigualdades entre expresiones algebraicas. A diferencia de las ecuaciones, que sólo se verifican para algunos valores de la variable, las inecuaciones tienen infinitas soluciones.
PROPIEDADES CON DESIGUALDADES.
· Si a los dos miembros de una desigualdad les sumamos o restamos un mismo número la desigualdad se mantiene.
Concepto.- Las inecuaciones son desigualdades entre expresiones algebraicas. A diferencia de las ecuaciones, que sólo se verifican para algunos valores de la variable, las inecuaciones tienen infinitas soluciones.
PROPIEDADES CON DESIGUALDADES.
· Si a los dos miembros de una desigualdad les sumamos o restamos un mismo número la desigualdad se mantiene.

· Si a los dos miembros de una desigualdad les multiplicamos o dividimos por un
mismo número, la desigualdad:
1. si el nº es positivo se mantiene:
mismo número, la desigualdad:
1. si el nº es positivo se mantiene:
3 <>
3(2)<5(2)>
6 <10>
2. si el nùmero es negativo, se invierte :
3<5
3(-2)>5(-2)
-6>-10
· Si elevamos los dos miembros de una desigualdad a un mismo
- Exponente impar la desigualdad se mantiene.
- Exponente par
· Si los términos son positivos la desigualdad se mantiene.
· Si los términos son negativos la desigualdad se invierte.
· Si uno es positivo y otro negativo depende de los valores
absolutos.
(Exponente impar):
· Si elevamos los dos miembros de una desigualdad a un mismo
- Exponente impar la desigualdad se mantiene.
- Exponente par
· Si los términos son positivos la desigualdad se mantiene.
· Si los términos son negativos la desigualdad se invierte.
· Si uno es positivo y otro negativo depende de los valores
absolutos.
(Exponente impar):
(Exponente par):
términos positivos:
términos negativos:
términos de distinto signo:
RESOLUCIÓN DE INECUACIONES DE PRIMER GRADO.
Son de la forma a x + b <0>
Son de la forma a x + b <0>
Ejemplo:
Interpretación geométrica.
La solución de una inecuación de primer grado representa aquellos valores de x que hacen que la función y = ax + b quede por encima del eje x (o por encima y sobre el propio eje x, o por debajo del eje x, o por debajo y sobre el propio eje x).
representa aquellos valores de x que hacen que la función y = ax + b quede por encima del eje x (o por encima y sobre el propio eje x, o por debajo del eje x, o por debajo y sobre el propio eje x).
Como podemos observar en las siguientes graficas:


La solución de una inecuación de primer grado
 representa aquellos valores de x que hacen que la función y = ax + b quede por encima del eje x (o por encima y sobre el propio eje x, o por debajo del eje x, o por debajo y sobre el propio eje x).
representa aquellos valores de x que hacen que la función y = ax + b quede por encima del eje x (o por encima y sobre el propio eje x, o por debajo del eje x, o por debajo y sobre el propio eje x).Como podemos observar en las siguientes graficas:


INECUACIONES DE SEGUNDO GRADO.
Presentan la forma ( ó £0 ó <0>

INECUACIONES DE GRADO SUPERIOR.
Se descomponen en factores de primer o segundo grado.
Se obtienen los ceros de cada factor representándolos en rectas distintas.
Se estudia el signo de cada uno de los intervalos formados.
En una nueva recta se llevan todos los ceros, aplicando la regla de los signos.
Se ve cuales de los intervalos son solución de la inecuación.
INECUACIONES FRACCIONARIAS.
Se obtienen por separado los ceros del numerador y denominador.
Se representan en sendas rectas.
En una nueva recta se llevan todos los ceros, aplicando la regla de los signos.
Se ve cuales de los intervalos formados son solución.
Los ceros del denominador nunca forman parte de la solución, al no estar
definida la división entre cero.
INECUACIONES CUADRATICAS.
Definición.- Sean a, b, c constantes reales tales que a ≠ 0. Sea x una variable real. Llamaremos inecuación cuadrática a toda inecuación en la cual uno de sus miembros es una expresión de la forma y el otro miembro es cero.
y el otro miembro es cero.
Son inecuaciones cuadráticas:
Presentan la forma ( ó £0 ó <0>
Para resolverlas se obtienen las raíces del trinomio de 2º grado  , y se estudía que intervalo/s de los obtenidos cumplen la inecuación, teniendo en cuenta que los intervalos externos tienen el signo de a y el intervalo interno signo contrario al de a. También se pueden resolver por factorización, obteniendo la solución de cada factor, calculando posteriormente la intersección de las soluciones.
, y se estudía que intervalo/s de los obtenidos cumplen la inecuación, teniendo en cuenta que los intervalos externos tienen el signo de a y el intervalo interno signo contrario al de a. También se pueden resolver por factorización, obteniendo la solución de cada factor, calculando posteriormente la intersección de las soluciones.
 , y se estudía que intervalo/s de los obtenidos cumplen la inecuación, teniendo en cuenta que los intervalos externos tienen el signo de a y el intervalo interno signo contrario al de a. También se pueden resolver por factorización, obteniendo la solución de cada factor, calculando posteriormente la intersección de las soluciones.
, y se estudía que intervalo/s de los obtenidos cumplen la inecuación, teniendo en cuenta que los intervalos externos tienen el signo de a y el intervalo interno signo contrario al de a. También se pueden resolver por factorización, obteniendo la solución de cada factor, calculando posteriormente la intersección de las soluciones. 
INECUACIONES DE GRADO SUPERIOR.
Se descomponen en factores de primer o segundo grado.
Se obtienen los ceros de cada factor representándolos en rectas distintas.
Se estudia el signo de cada uno de los intervalos formados.
En una nueva recta se llevan todos los ceros, aplicando la regla de los signos.
Se ve cuales de los intervalos son solución de la inecuación.
INECUACIONES FRACCIONARIAS.
Se obtienen por separado los ceros del numerador y denominador.
Se representan en sendas rectas.
En una nueva recta se llevan todos los ceros, aplicando la regla de los signos.
Se ve cuales de los intervalos formados son solución.
Los ceros del denominador nunca forman parte de la solución, al no estar
definida la división entre cero.
INECUACIONES CUADRATICAS.
Definición.- Sean a, b, c constantes reales tales que a ≠ 0. Sea x una variable real. Llamaremos inecuación cuadrática a toda inecuación en la cual uno de sus miembros es una expresión de la forma
 y el otro miembro es cero.
y el otro miembro es cero.Son inecuaciones cuadráticas:
La resolución de las inecuaciones es muy parecida a la resolución de las ecuaciones.
Inecuaciones de grado superior a dos
Se descomponen en inecuaciones de grado uno y dos.
Inecuaciones fraccionarias
Son las inecuaciones en las que tenemos la incógnita en el denominador.
Se pasan todos los términos a un lado del signo de desigualdad y se reducen a común denominador.
Después se buscan las soluciones y estudiamos el signo (como en el caso de las ecuaciones de segundo grado). Hay que tener en cuenta que las soluciones que anulan el denominador no valen.
Se descomponen en inecuaciones de grado uno y dos.
Inecuaciones fraccionarias
Son las inecuaciones en las que tenemos la incógnita en el denominador.
Se pasan todos los términos a un lado del signo de desigualdad y se reducen a común denominador.
Después se buscan las soluciones y estudiamos el signo (como en el caso de las ecuaciones de segundo grado). Hay que tener en cuenta que las soluciones que anulan el denominador no valen.




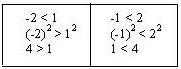




No hay comentarios:
Publicar un comentario